Size-based particle separation for biomedical technologies
We developed a dynamical systems framework for inertial microfluidics, providing a predictive theory for particle focusing, bifurcations, and size-based particle separation in curved microchannels. This work enables the rational design of microfluidic devices for applications such as biomedical diagnostics and industrial particle separators, and connects applied mathematics directly with experimental microfluidic platforms.
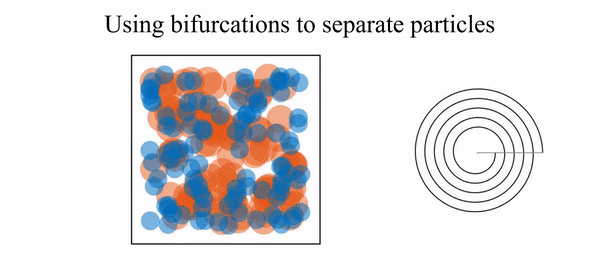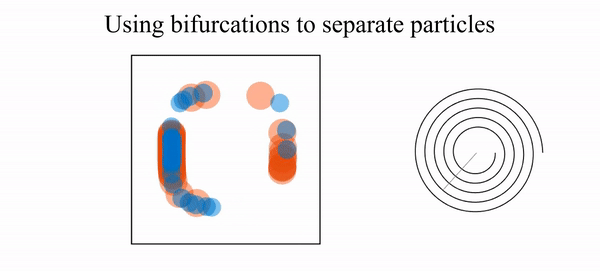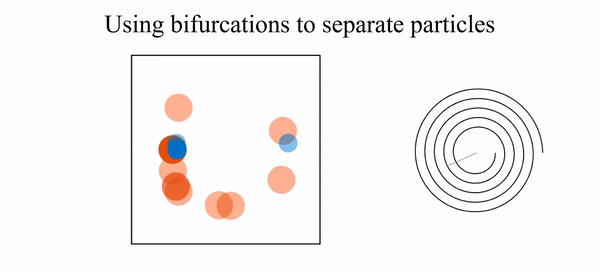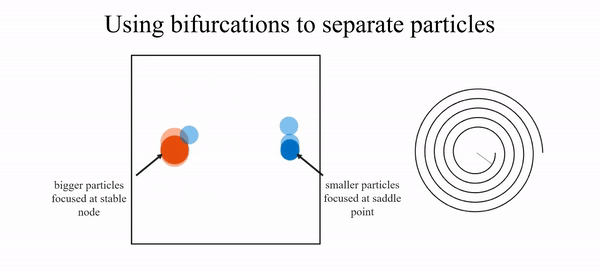
- R. N. Valani, B. Harding and Y. M. Stokes, Inertial particle focusing in fluid flow through spiral ducts: dynamics, tipping phenomena and particle separation, Journal of Fluid Mechanics, 990, A13 (2024) arXiv
- R. N. Valani, B. Harding and Y. M. Stokes, Utilizing bifurcations to separate particles in spiral inertial microfluidics, Physics of Fluids, 35, 011703 (2023) arXiv
- R. N. Valani, B. Harding and Y. M. Stokes, Bifurcations and dynamics in inertial focusing of particles in curved rectangular ducts, SIADS, 21, 2371-2392 (2022)arXiv
Biological active matter: active nematics & tissue mechanics
We study theoretical and computational models of biological active matter, with a focus on active nematics and vertex-based descriptions of tissues. Our research addresses how nonequilibrium forcing, deformability, and internal stresses give rise to emergent order, flow instabilities, and intermittent collective migration. Current work includes modelling tissue-scale dynamics in developing embryos and understanding bifurcations and rheology in confined active nematic systems.

- Ioannis Hadjifrangiskou, Sumesh P. Thampi and R. N. Valani, Nematic order from phase synchronization of shape oscillations, Physical Review Letters, 135, 068101 (2025) arXiv
- R. N. Valani, Sumesh Thampi and Julia M. Yeomans, From Equilibrium Multistability to Spatiotemporal Chaos in Channel Flows of Nematic Fluids. (under review) arXiv
Synthetic active matter: superwalking droplets
Superwalking droplets are self-propelled liquid drops that bounce and walk on a vertically vibrated fluid bath, forming a novel class of synthetic active matter in which each droplet acts as an energy consuming particle powered by its interaction with a self-generated wave field. Unlike many synthetic active systems with constant self-propulsion, superwalking droplets exhibit rich internal-state dynamics, including transitions between stationary, steady, and oscillatory motion, driven by memory effects in the wave–particle coupling. Such active wave-particle entities exhibit hydrodynamic analogs of quantum systems.






- R. N. Valani, A. C. Slim and T. Simula, Superwalking droplets, Physical Review Letters, 123, 024503 (2019) arXiv
- R. N. Valani, J. Dring, A.C. Slim and T. Simula, Emergence of superwalking droplets, Journal of Fluid Mechanics, 906, A3 (2021) arXiv
- R. N. Valani and David M. Paganin, Active wave-particle clusters. Physical Review E, 112, 065103 (2025) arXiv
Microswimmers in fluid flows
We study the dynamics of microswimmers and active particles in background flows using reduced dynamical systems that admit a Hamiltonian structure. In channel flows, this formalism reveals conserved quantities and phase space organisation, allowing the classification of swimmer trajectories, bifurcations, and crossstream migration mechanisms that govern long-time transport and focusing.
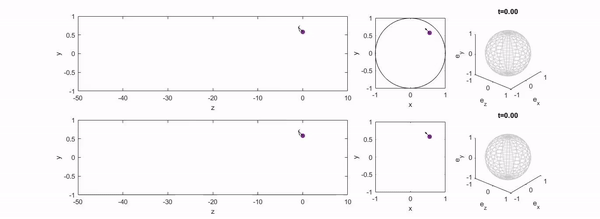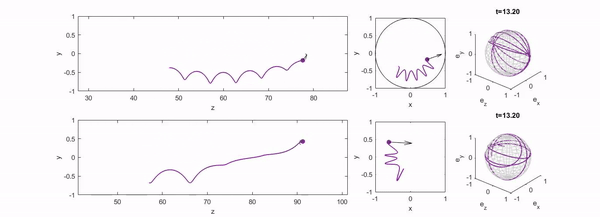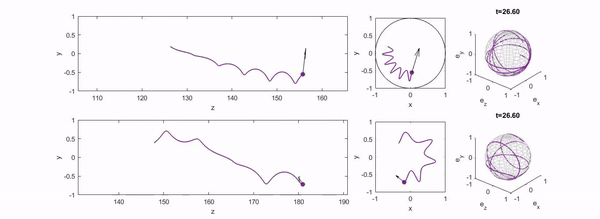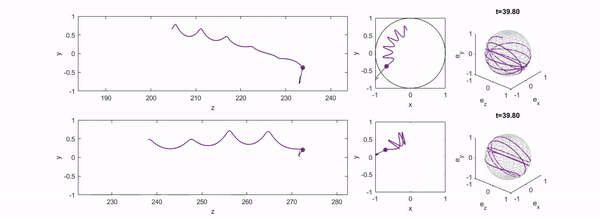
- B. Harding, R. N. Valani and Y. Stokes, Hamiltonian formulation for the motion of an active spheroidal particle suspended in laminar straight duct flow, Physical Review E, 112, 054125 (2025) arXiv
- R. N. Valani, B. Harding and Y. M. Stokes, Active particle motion in Poiseuille flow through rectangular channels, Physical Review E, 110, 034603 (2024) arXiv
Active matter with individual complexity
Murmurations of birds, schools of fish, insect swarms, bacterial suspensions, human crowds, and robotic swarms are all examples of complex collective behaviours that emerge from interactions among individuals. We introduce a class of active systems, termed attractor-driven matter, in which each particle’s internal complexity is represented by an internal state evolving on an attracting set of a chaotic dynamical system. This framework gives rise to rich individual and collective dynamics, including multistability, anomalous transport, and emergent organisation. The formalism provides a flexible and general approach for generating complex dynamical and collective behaviours across a wide range of physical, biological, and engineered systems.
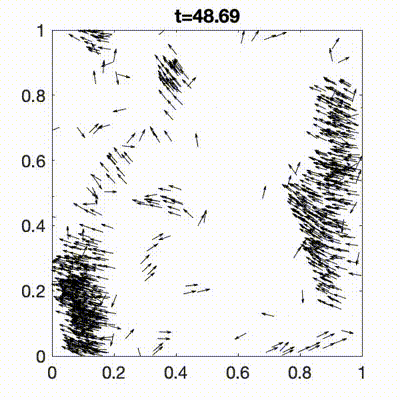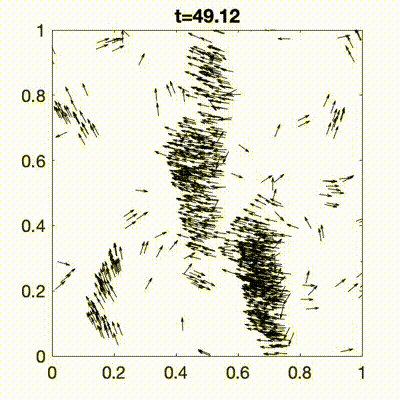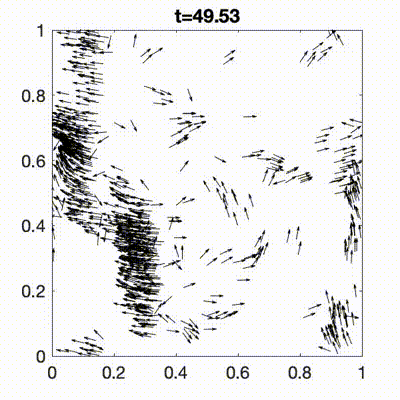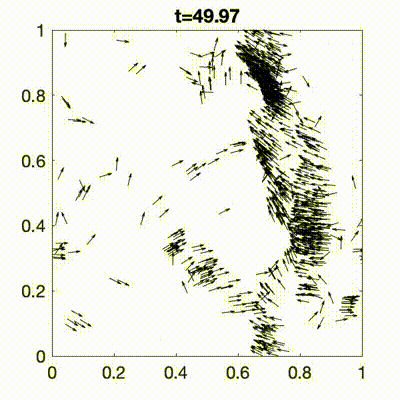
- R. N. Valani and D. M. Paganin, Attractor-driven matter, Chaos, 33, 023125 (2023) arXiv Talk
- R. N. Valani, Infinite-memory classical wave-particle entities, attractor-driven active particles and the diffusionless Lorenz equations, Chaos, 34, 013133 (2024) arXiv
- R. N. Valani and B. Dandogbessi, Asymmetric limit cycles within Lorenz chaos induce anomalous mobility for a memory-driven active particle, Physical Review E (Letter), 110, L052203 (2024) arXiv
Dynamical origins of hydrodynamic quantum analogs
We investigate the dynamical foundations of hydrodynamic quantum analogs in walking droplet using minimal dynamical models. Using reduced Lorenz-like dynamical descriptions derived from integrodifferential trajectory equations, we show how quantum-like statistical signatures such as Friedel-like oscillations, quantization, and tunnelling analogs, can emerge from purely local perturbations of the particle’s internal dynamical state. This perspective reveals a generic, attractor-driven route to quantum-like behaviour rooted in nonlinear dynamics, without requiring explicitly nonlocal wave-mediated interactions.

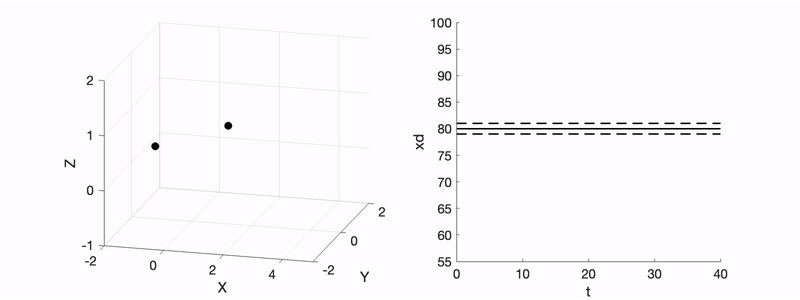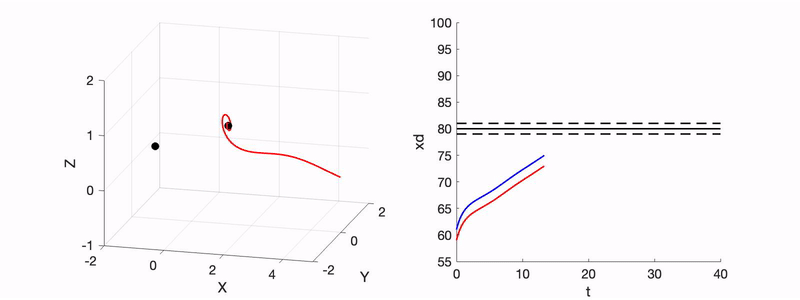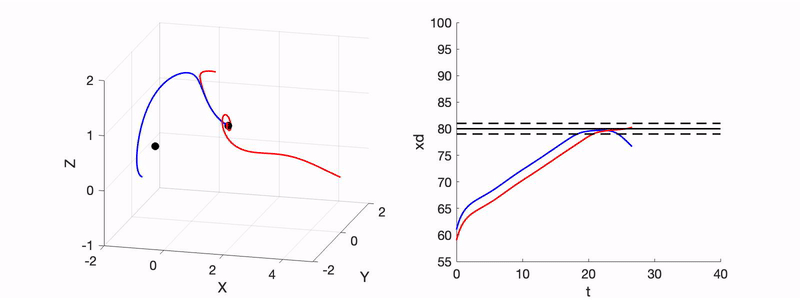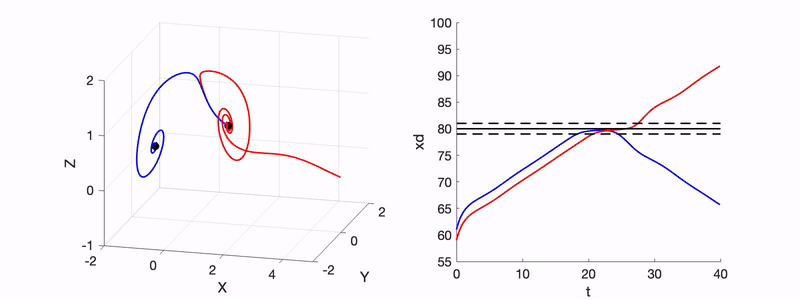
- R. Xu and R. N. Valani, Tunneling in a Lorenz-like model for an active wave-particle entity, Physical Review E, 111, 034218 (2025) arXiv
- R. N. Valani and A. G. López, Quantum-like behavior of an active particle in a double-well potential, Chaos, Solitons & Fractals, 186, 115253 (2024) arXiv
- R. N. Valani, Lorenz-like systems emerging from an integro-differential trajectory equation of a one-dimensional wave-particle entity, Chaos, 32, 023129 (2022) arXiv
Collaborators
- Julia Yeomans (University of Oxford, UK)
- Sumesh Thampi (IIT Madras, India)
- Tapio Simula (Swinburne University of Technology, Australia)
- Anja Slim (Monash University, Australia)
- Mohit Dalwadi (University of Oxford, UK)
- Benjamin Walker (University College London, UK)
- Shankar Srinivas (University of Oxford, UK)
- David Paganin (Monash University, Australia)
- Álvaro López (Universidad Rey Juan Carlos, Spain)
- David Müller-Bender (Chemnitz University of Technology, Germany)
- Yvonne Stokes (Adelaide University, Australia)
- Brendan Harding (Victoria University of Wellington, New Zealand)
- Divya Jaganathan (Harvard University, USA)
- Rainer Klages (Queens Mary University of London, UK)
- Esa Räsänen (Tampere University, Finland)
- Aditya S. Khair (Carnegie Mellon University, USA)
- Bruno S. Dandogbessi (UNSTIM, Benin)
- Antarip Poddar (IIT Dhanbad, India)
- Aritra Roy (IIT Bombay, India)
- Yuanmei Li (Nanjing University, China)
- Titir Mukherjee (IISER Kolkata, India)
- Soumitro Banerjee (IISER Kolkata, India)
- Matthew Durey (University of Glasgow, UK)
- Diogo Pinto (University of Lisbon, Portugal)
