Preprints
- Titir Mukherjee, Rahil N. Valani, and Soumitro Banerjee, Active Soft-Impact Oscillator: Dynamics of a Walking Droplet in a Non-Smooth Potential. (under review) arXiv
- Ioannis Hadjifrangiskou, Rahil N. Valani, and Diogo E. P. Pinto, Shear-Induced Collective Shape Oscillations in Dense Soft Suspensions. (under review) arXiv
- Rahil N. Valani, Emergence of Friedel-like oscillations from Lorenz dynamics in walking droplets. (under review) arXiv
- Rudra Sekhri, Rahil N. Valani, and Tapio Simula, Intermittent Motility of a Synthetic Active Particle in Changing Environments. (under review) arXiv
- Rahil N. Valani, Sumesh Thampi and Julia M. Yeomans, From Equilibrium Multistability to Spatiotemporal Chaos in Channel Flows of Nematic Fluids. (under review) arXiv
2025
- Rahil N. Valani and David M. Paganin, Active wave-particle clusters. Physical Review E, 112, 065103 (2025) arXiv

We use numerical simulations to show that self-propelled droplets can spontaneously form stable, nucleus-like clusters through wave-mediated interactions. These active clusters exhibit collective motion, deformation, and decay processes analogous to vibrational, rotational, and radioactive phenomena in nuclear systems, revealing emergent quantum-like behaviour in active matter.
- D. Müller-Bender and R. N. Valani, Laminar chaos in systems with random and chaotically time-varying delay Physical Review E, 112, 064203 (2025) arXiv
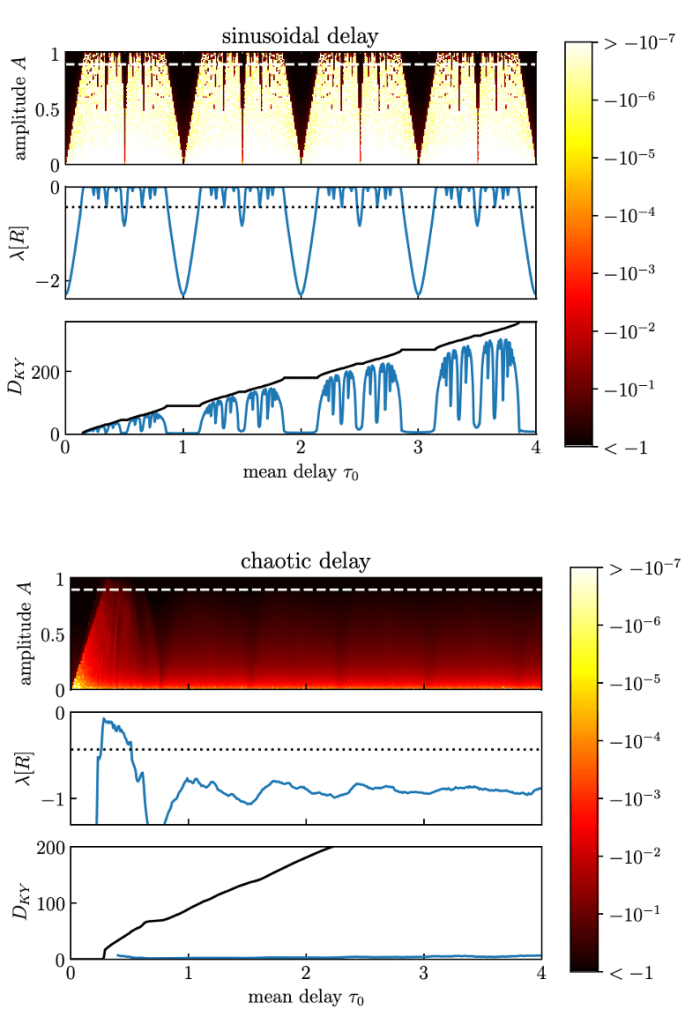
We show that laminar chaos, characterised by long quiescent phases interrupted by bursts, can arise not only from periodically varying time delays, but also from randomly or chaotically varying delays. The results demonstrate that laminar chaos originates from a resonance with a system’s own past and provide practical tools to identify it and distinguish it from related phenomena in experimental data.
- Divya Jaganathan and R. N. Valani, Markovian embedding of nonlocal equations using spectral representation. Communications in Nonlinear Science and Numerical Simulation, 109540 (2025) arXiv
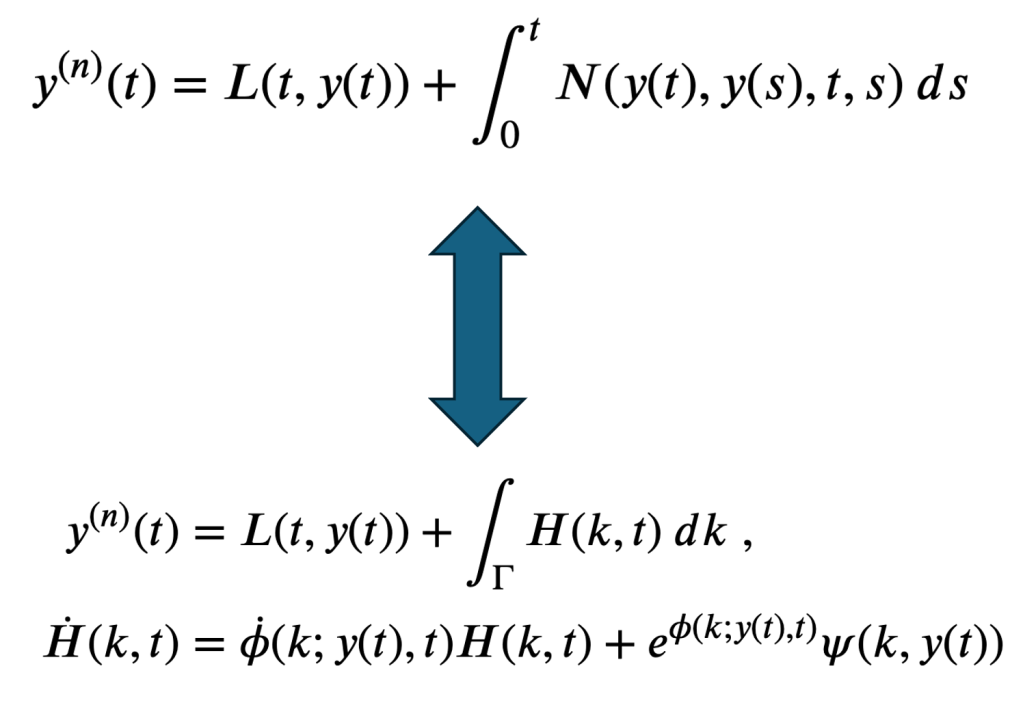
We show that a broad class of nonlinear, history-dependent equations can be reformulated in a fully local, Markovian form using a spectral representation of the memory kernel. By introducing a small set of auxiliary variables, the approach exactly captures memory effects without requiring storage of the full past.
- B. Harding, R. N. Valani and Y. Stokes, Hamiltonian formulation for the motion of an active spheroidal particle suspended in laminar straight duct flow, Physical Review E, 112, 054125 (2025) arXiv
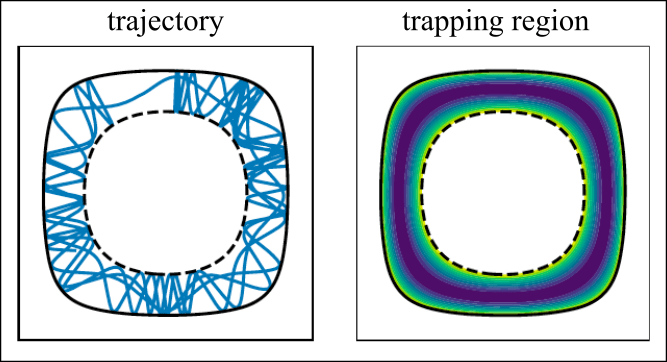
We develop a unified mathematical framework to describe the motion of microswimmers (e.g. microorganisms or microrobots) in steady channel flows of varying cross-section. Despite complex trajectories, particles of different shapes remain confined to well-defined, predictable regions, revealing hidden structure in active transport through fluids.
- Jason K. Kabarowski, Aditya S. Khair and Rahil N. Valani, Hydrodynamic memory and Quincke rotation, Physical Review Fluids, 10, 093701 (2025) arXiv
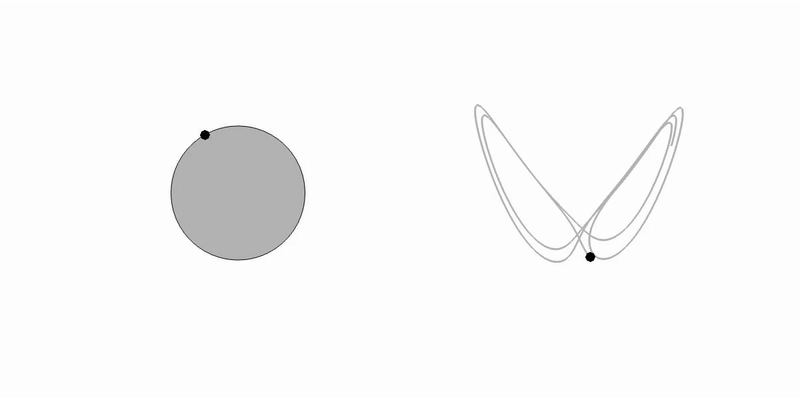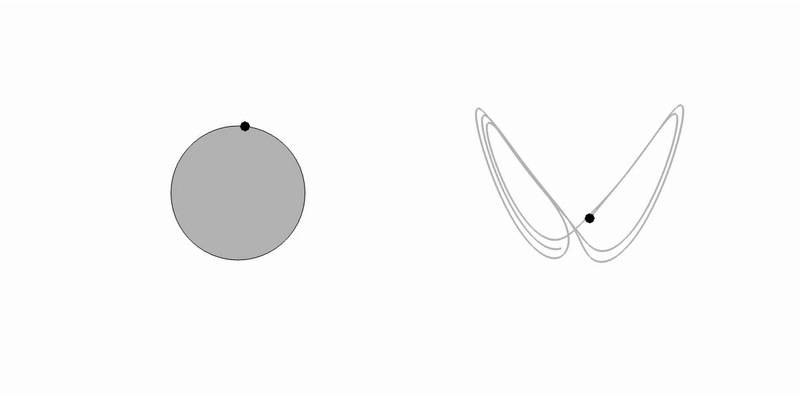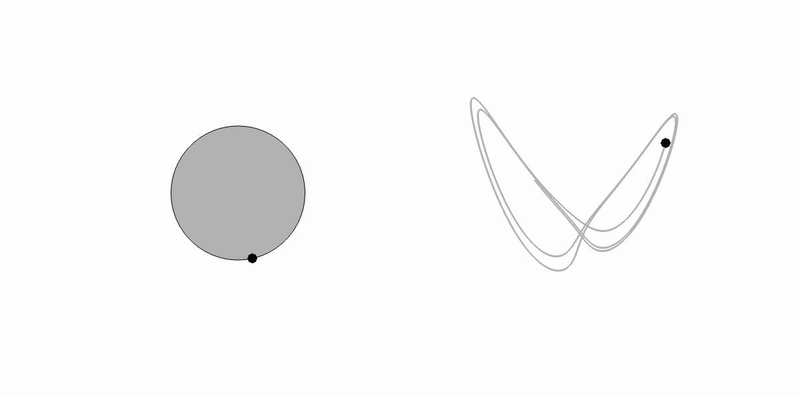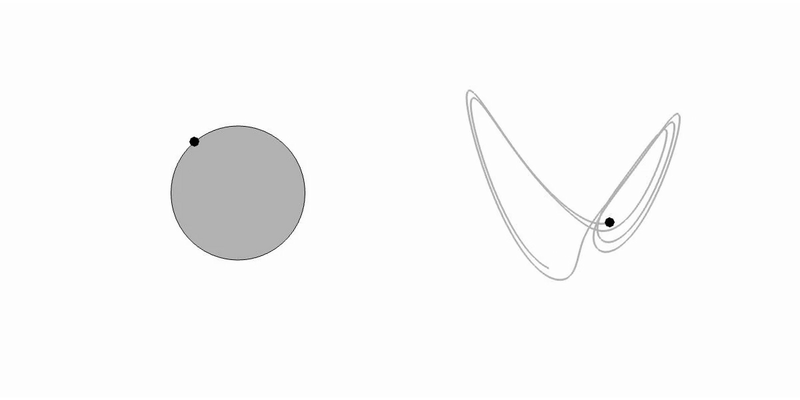
We show that incorporating fluid inertia into the Lorenz description of Quincke rotation leads to “memory Lorenz” equations that reconcile theory with experiments. Memory effects delay the onset of chaos, enhance multistability, and can restore periodic motion, with broader implications for Lorenz-type systems and chaos control in active matter.
- Ioannis Hadjifrangiskou, Sumesh P. Thampi and Rahil N. Valani, Nematic order from phase synchronization of shape oscillations, Physical Review Letters, 135, 068101 (2025) arXiv

We show that deformable elongated particles in oscillatory shear flow can synchronize their shape oscillations and spontaneously form nematic order, even in the absence of particle–particle interactions. This behaviour arises from phase-locking between particle deformation and the driving flow and is absent in rigid particles.
- A. G. López and R. N. Valani, Driven transitions between megastable quantized orbits, Chaos, Solitons & Fractals, 198, 116549 (2025) arXiv
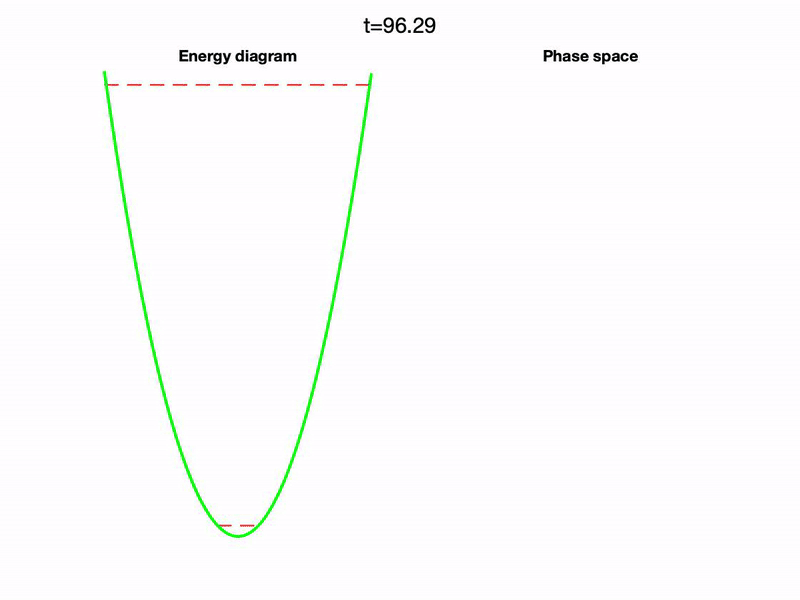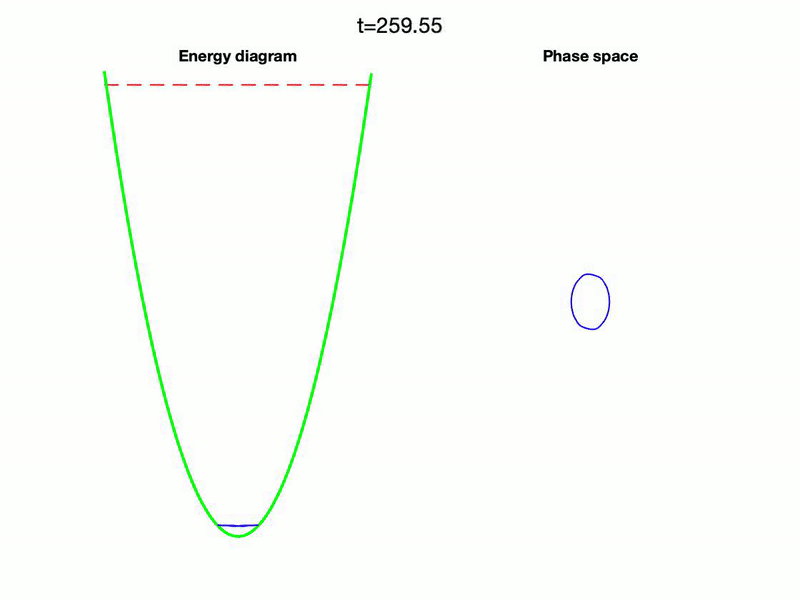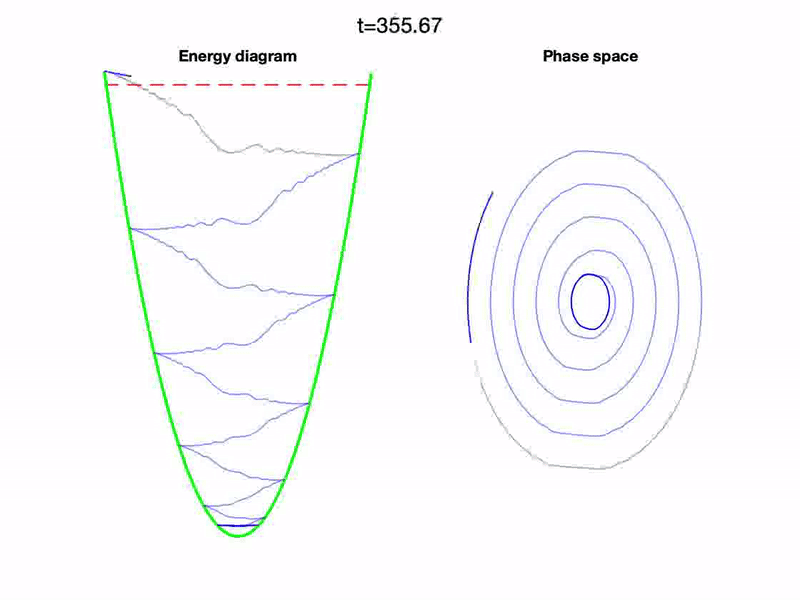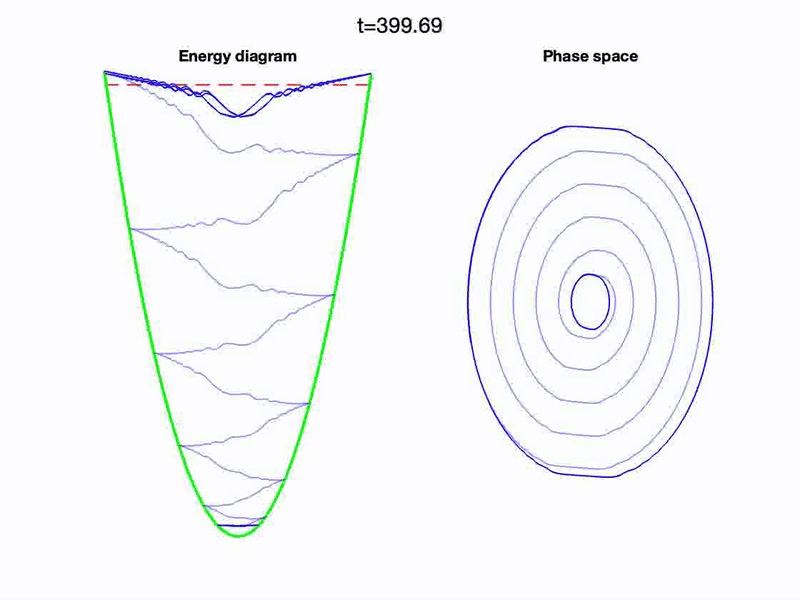
We show that a nonlinear oscillator with state-dependent delay can exhibit an infinite hierarchy of nested limit-cycle attractors (megastability) and undergo controlled transitions between quantized orbits under external driving. Resonance and beating enable upward and downward transitions between these states, forming a classical analogue of quantum jumps with potential applications in multistable engineering systems.
- R. Xu and R. N. Valani, Tunneling in a Lorenz-like model for an active wave-particle entity, Physical Review E, 111, 034218 (2025) arXiv
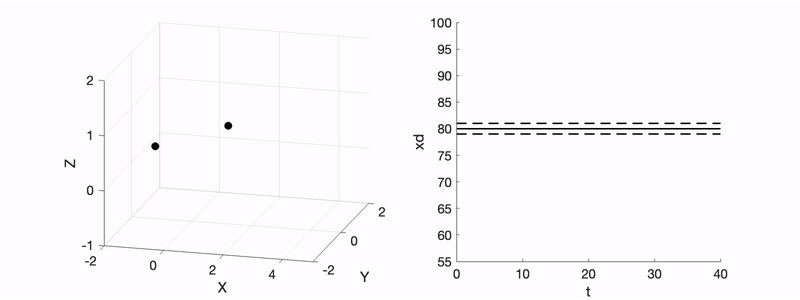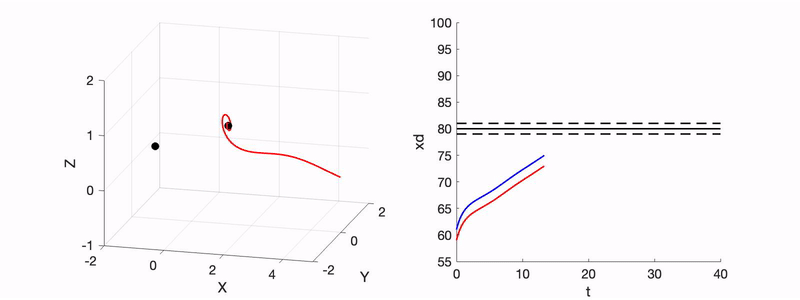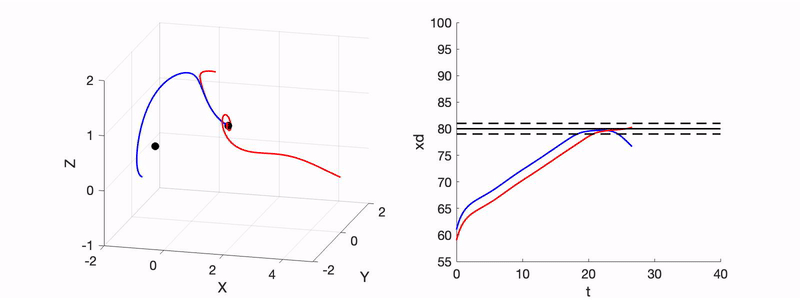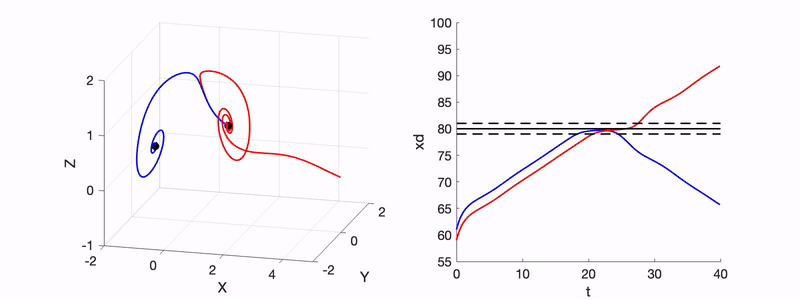
We show that a classical active wave–particle system encountering a barrier can exhibit unpredictable tunneling due to its mapping onto a perturbed Lorenz system. Nonlinear dynamics and sensitivity to initial conditions enable barrier crossing without energy conservation, providing a classical analogue of tunneling.
- A. G. López and R. N. Valani, Megastable quantization in generalized pilot-wave hydrodynamics, Physical Review E (Letter), 111, L022201 (2025) arXiv
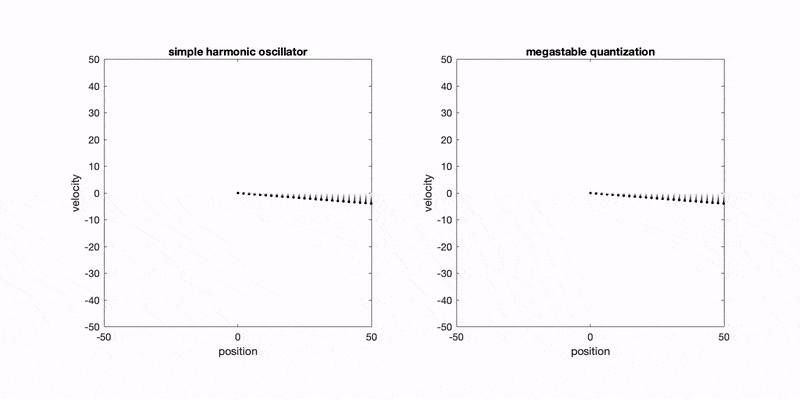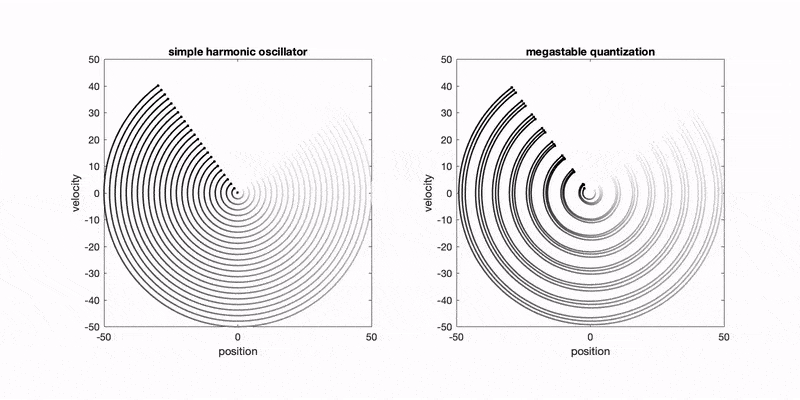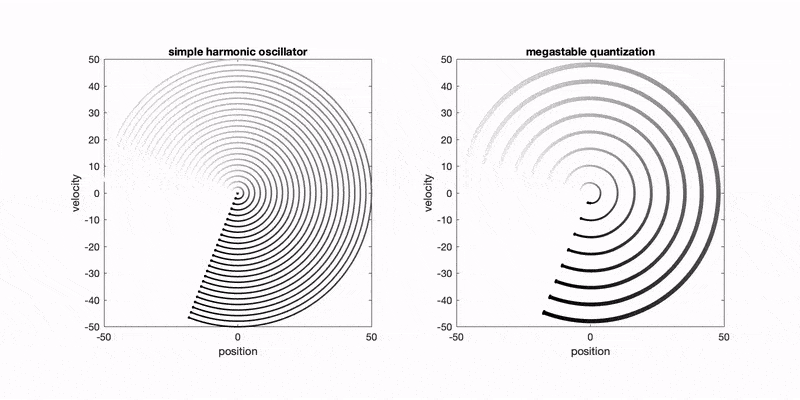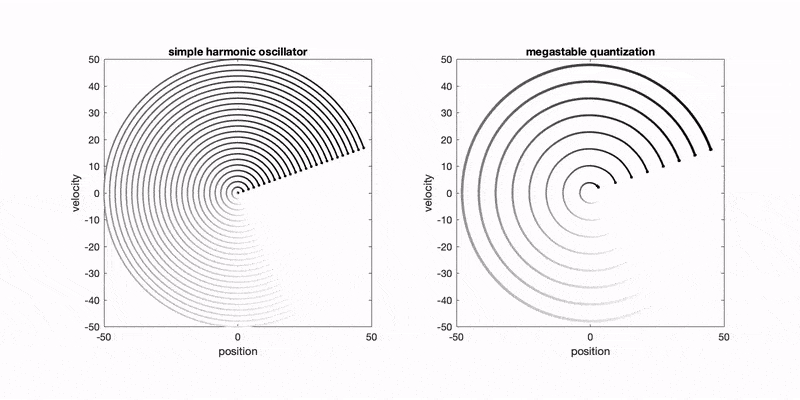
We show that a classical pilot-wave model with truncated memory can produce a countably infinite set of coexisting limit-cycle states (megastability) in a harmonic potential. This provides a classical analogue of quantized energy levels arising from nonconservative, oscillatory forcing.
2024
- R. N. Valani and B. Dandogbessi, Asymmetric limit cycles within Lorenz chaos induce anomalous mobility for a memory-driven active particle, Physical Review E (Letter), 110, L052203 (2024) arXiv Talk
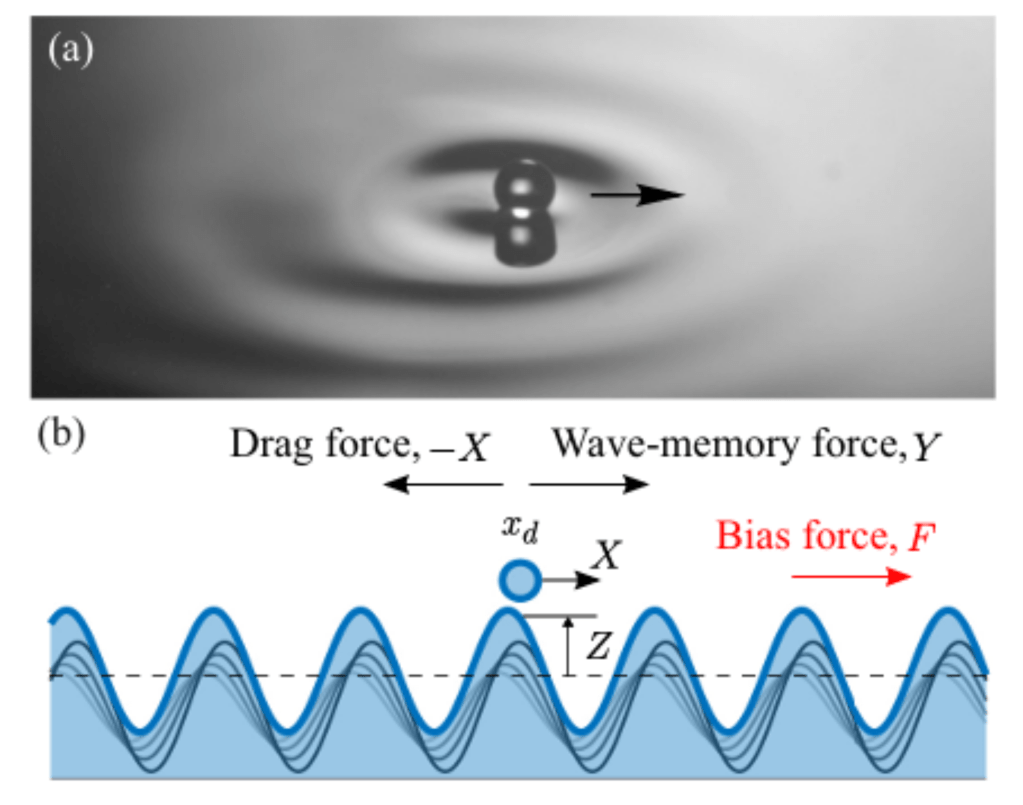
We identify a dynamical mechanism for negative mobility in a memory-driven active particle by mapping its motion to a biased Lorenz system. A small applied force can induce transport opposite to the bias, revealing how low-dimensional nonlinear dynamics generate anomalous transport in active matter.
- R. N. Valani, B. Harding and Y. M. Stokes, Active particle motion in Poiseuille flow through rectangular channels, Physical Review E, 110, 034603 (2024) arXiv
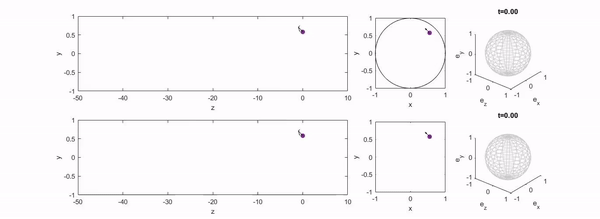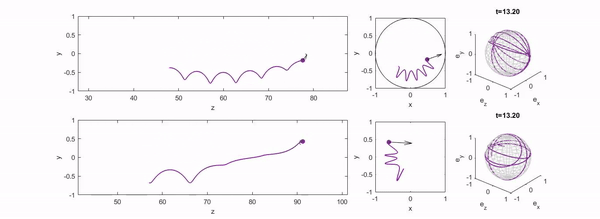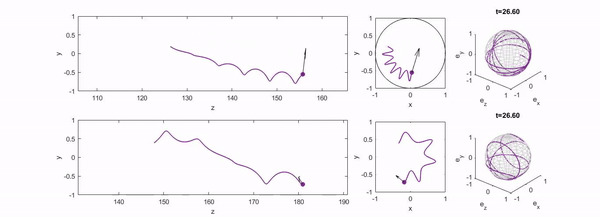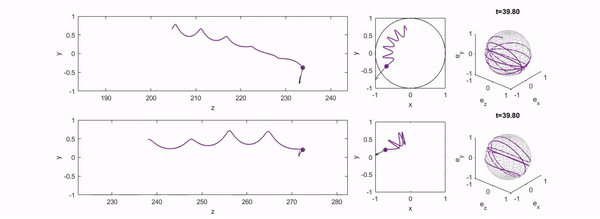
We study the motion of an active particle in channel flow and identify a range of regular and chaotic trajectories, including swinging, trapping, tumbling, and wandering states. These results provide insight into the dynamics of natural and artificial microswimmers in confined environments.
- R. N. Valani, B. Harding and Y. M. Stokes, Inertial particle focusing in fluid flow through spiral ducts: dynamics, tipping phenomena and particle separation, Journal of Fluid Mechanics, 990, A13 (2024) arXiv

We identify tipping points in the dynamics of particles flowing through spiral microfluidic channels and show how these transitions can be exploited to control particle trajectories. This provides new strategies for optimising size-based particle separation in biomedical and industrial microfluidic devices.
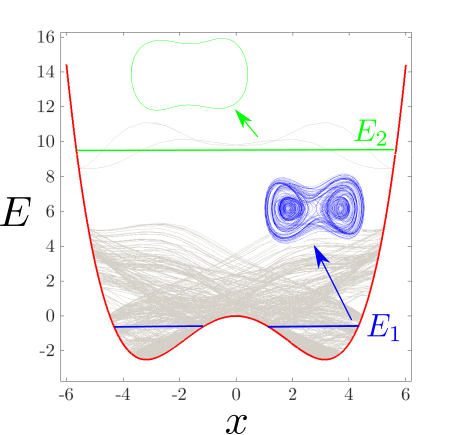
- R. N. Valani and A. G. López, Quantum-like behavior of an active particle in a double-well potential, Chaos, Solitons & Fractals, 186, 115253 (2024) arXiv

We show that a simple mathematical model of a self-propelled droplet interacting with its own wave field can exhibit quantum-like behaviour in a double-well potential. The system displays multistable quantized states, intermittent tunnelling, and wave-like statistics, despite being entirely classical.
- B. Harding, Y. Stokes and R. N. Valani, Inertial focusing dynamics of spherical particles in curved microfluidic ducts with a trapezoidal cross-section, SIADS, 23, 1805-1835 (2024) arXiv
- R. N. Valani, B. Harding and Y. M. Stokes, Bifurcations in inertial focusing of a particle suspended in flow through curved rectangular ducts Perspectives in Dynamical Systems II — Numerical and Analytical Approaches. DSTA 2021. Springer Proceedings in Mathematics & Statistics, vol 454. Springer, Cham. (2024) arXiv Talk

We analyse an ODE model for particle focusing in curved duct flows and identify equilibrium states and their bifurcations using analytical and numerical methods. Saddle-node, pitchfork, and Hopf bifurcations emerge as system parameters vary, with implications for the design of inertial microfluidic devices for size-based particle separation.
- A. G. López and R. N. Valani, Unpredictable tunneling in a retarded bistable potential, Chaos, 34, 043117 (2024) arXiv
We show that a particle subject to state-dependent delayed feedback in a double-well potential can exhibit multistability between distinct dynamical attractors forming an effective two-level system. Bifurcation analysis reveals chaotic transitions between wells driven by crisis-induced intermittency, providing a dynamical explanation for tunnelling-like behaviour.
- R. N. Valani, Infinite-memory classical wave-particle entities, attractor-driven active particles and the diffusionless Lorenz equations, Chaos, 34, 013133 (2024) arXiv Talk
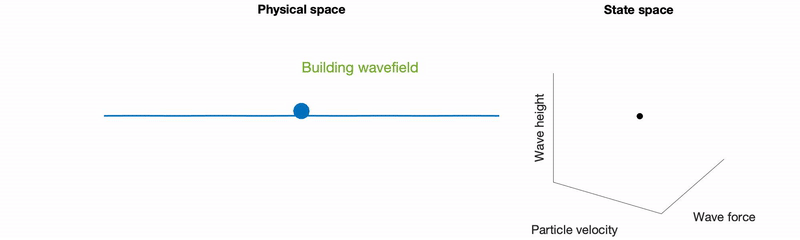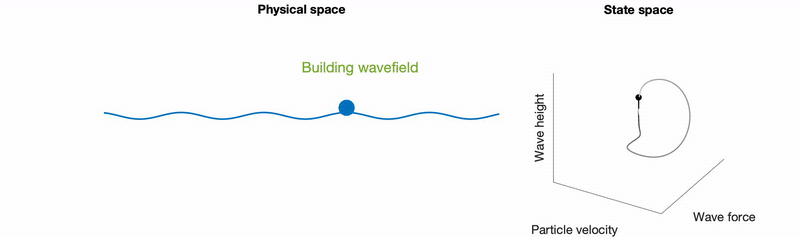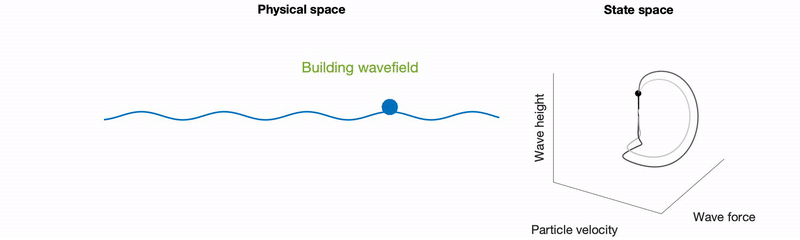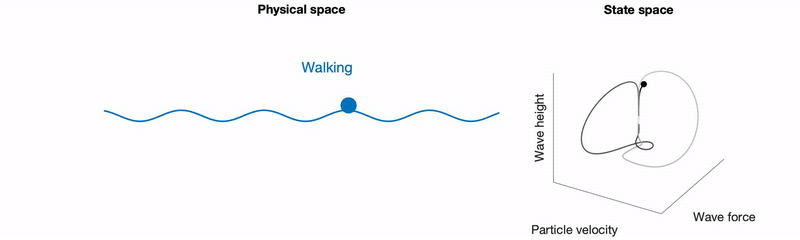
We show that a high-memory model of a walking droplet reduces to the diffusionless Lorenz equations, forming a minimal example of an attractor-driven active particle. Linking the phase-space geometry and bifurcations of the Lorenz system to particle motion provides new insight into hydrodynamic quantum analogues and active particle dynamics.
2023
- J. Perks and R. N. Valani, Dynamics, interference effects and multistability in a Lorenz-like system of a classical wave-particle entity in a periodic potential, Chaos, 33, 033147 (2023) arXiv
We analyse a Lorenz-like model of a classical wave–particle entity in a sinusoidal potential and identify a rich set of steady and unsteady motions, including oscillatory, runaway, and irregular dynamics. The system exhibits interference-like patterns and multistability in parameter space, drawing analogies with Bragg reflection and electron motion in crystals.
- R. N. Valani and D. M. Paganin, Attractor-driven matter, Chaos, 33, 023125 (2023) arXiv Talk

We introduce a formalism in which a particle’s dynamics are driven directly by an attractor in its internal state space, giving rise to a new class of systems termed attractor-driven matter. This framework generates rich single-particle and collective behaviours reminiscent of active matter and provides a flexible way to model complex dynamical systems.
- D. Müller-Bender, R. N. Valani, G. Radons, Pseudo-laminar chaos from on-off intermittency, Physical Review E, 107, 014208 (2023) arXiv
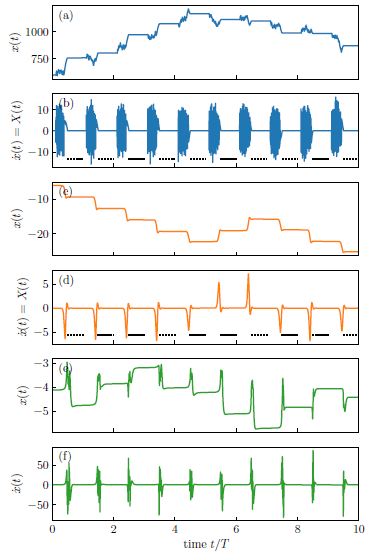
We distinguish true laminar chaos from visually similar diffusion-like dynamics in Lorenz-type wave–particle systems, introducing the concept of pseudolaminar chaos. While the two behaviours appear nearly indistinguishable at the signal level, correlation analysis reveals clear dynamical differences, even in the presence of noise.
- R. N. Valani, B. Harding and Y. M. Stokes, Utilizing bifurcations to separate particles in spiral inertial microfluidics, Physics of Fluids, 35, 011703 (2023) arXiv
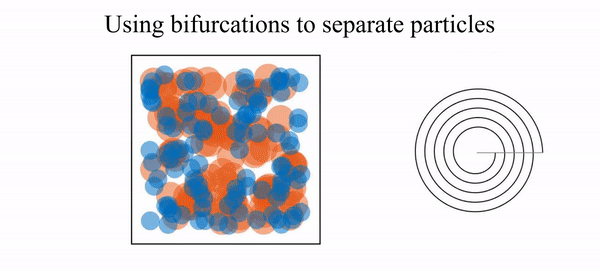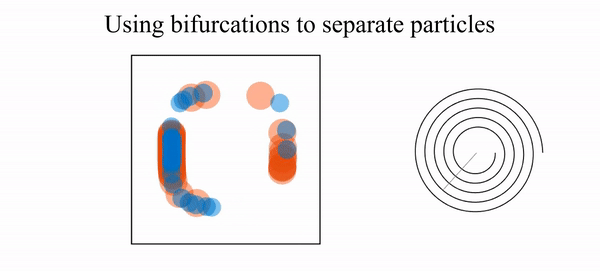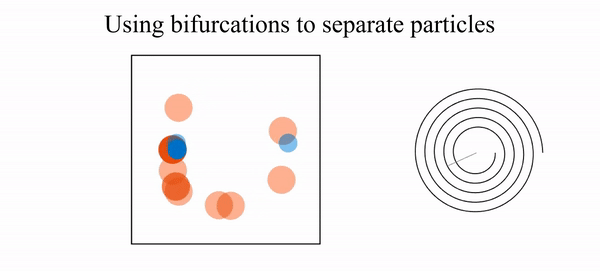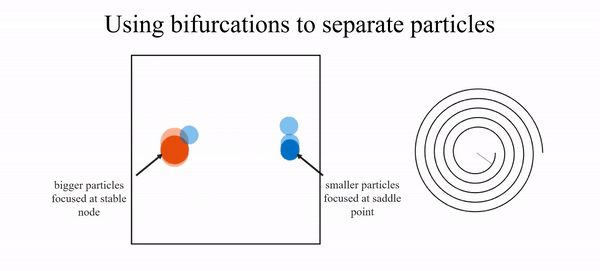
We show that particle focusing in curved duct flows undergoes bifurcations as the duct curvature varies, arising from the balance between inertial lift and vortex-induced drag. Exploiting these bifurcations in spiral ducts enables enhanced size-based particle separation, including a mechanism based on transient trapping near saddle points.
2022
- R. N. Valani, B. Harding and Y. M. Stokes, Bifurcations and dynamics in inertial focusing of particles in curved rectangular ducts, SIADS, 21, 2371-2392 (2022) arXiv Talk

We develop an asymptotic model for particle focusing in curved duct flows, revealing how inertial lift and curvature-induced vortices produce multiple equilibrium states. Bifurcation analysis identifies parameter regimes that optimise size-based particle separation, with direct relevance to microfluidic technologies such as circulating tumour cell isolation.
- R. N. Valani, Lorenz-like systems emerging from an integro-differential trajectory equation of a one-dimensional wave-particle entity, Chaos, 32, 023129 (2022) arXiv Kudos

We show that the trajectory equations of walking droplets can reduce to Lorenz-like dynamical systems for certain wave configurations. This provides a dynamical-systems framework for understanding how chaotic dynamics give rise to emergent statistical behaviour in hydrodynamic quantum analogues.
- R. N. Valani, Anomalous transport of a classical wave-particle entity in a tilted potential, Physical Review E, 105, L012101 (2022) arXiv Talk1 Talk2

We show that a simple model of a walking droplet can exhibit negative mobility, drifting opposite to an applied bias force due to memory-driven dynamics. This demonstrates that paradoxical transport can arise in self-propelled wave–particle systems without noise or periodic forcing.
2021
- R. N. Valani, A. C. Slim, D. M. Paganin, T. P. Simula, and T. Vo, Unsteady dynamics of a classical particle-wave entity, Physical Review E, 104, 015106 (2021) arXiv
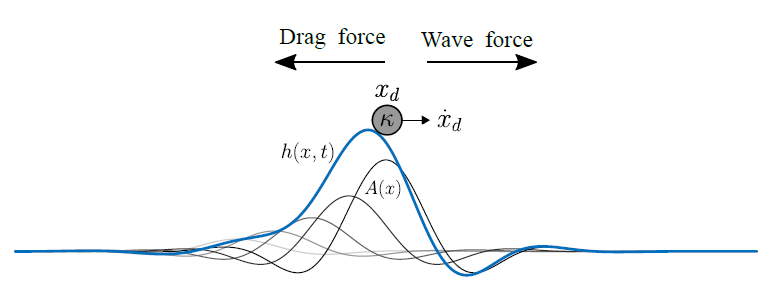
Using a one-dimensional pilot-wave model, we show that unsteady walking dynamics of a self-propelled droplet can be mapped onto the Lorenz system. This reveals connections between deterministic chaos, stochastic descriptions via Langevin dynamics, and diffusion-like behaviour in wave–particle systems.
- R. N. Valani, A.C. Slim and T. Simula, Stop-and-go locomotion of superwalking droplets, Physical Review E, 103, 043102 (2021) arXiv Talk
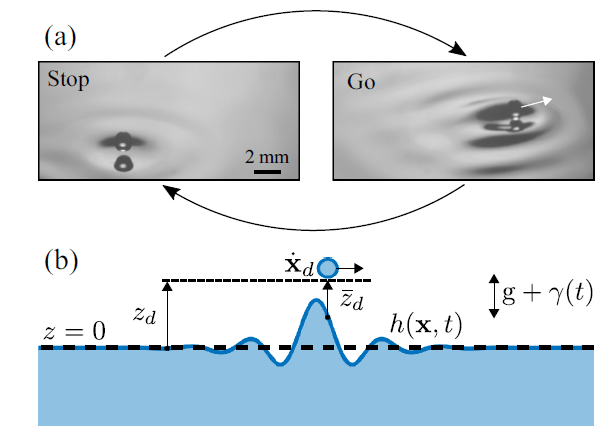
We numerically show that superwalking droplets driven by slowly varying phase differences between two forcing frequencies exhibit distinct forms of intermittent motion, including oscillatory, stop–and–go, and irregular dynamics. These results provide a foundation for controlling droplet trajectories through engineered time-dependent driving.
- R. N. Valani, J. Dring, A.C. Slim and T. Simula, Emergence of superwalking droplets, Journal of Fluid Mechanics, 906, A3 (2021) arXiv
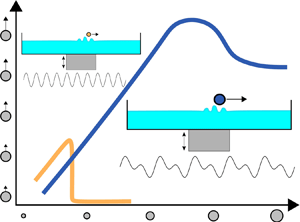
We develop a theoretical model for superwalking droplets driven by two-frequency vibration and explain how coupled vertical and horizontal dynamics give rise to sustained self-propulsion. Numerical results agree with experiments and clarify the mechanism underlying the emergence of superwalking states.
2020
- R. N. Valani, Superwalking Droplets and Generalised Pilot-Wave Dynamics, PhD Thesis, Monash University (2020)

Millimetre-sized walking droplets that emerge on the surface of a vertically vibrating liquid bath can exhibit certain features that were previously thought to be exclusive to the microscopic quantum realm. This thesis investigates a new class of walking droplets, coined superwalkers, and also studies the rich dynamical behaviour of droplets in a generalised pilot-wave framework. Insights from this research may help further our understanding in the areas of hydrodynamic quantum analogues and active matter.
2019
- R. N. Valani, A. C. Slim and T. Simula, Superwalking droplets, Physical Review Letters, 123, 024503 (2019) arXiv
- Superwalking droplets videos
A walker is a droplet of liquid that self-propels on the free surface of an oscillating bath of the same liquid through feedback between the droplet and its wave field. We have studied walking droplets in the presence of two driving frequencies and have observed a new class of walking droplets, which we coin superwalkers. Superwalkers may be more than double the size of the largest walkers, may travel at more than triple the speed of the fastest ones, and enable a plethora of novel multidroplet behaviors.
2018
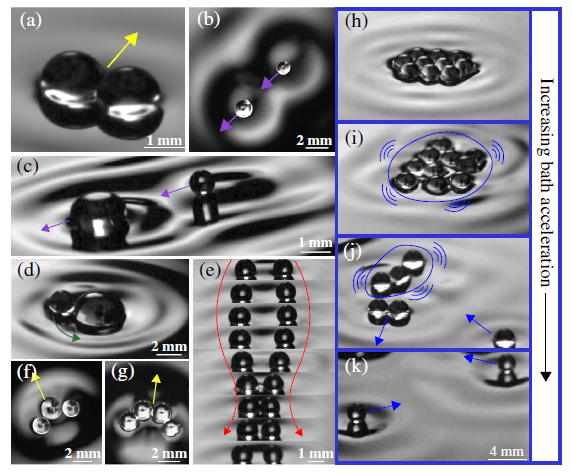
- R. N. Valani and A.C. Slim, Pilot-wave dynamics of two identical, in-phase bouncing droplets, Chaos, 28 (9), 096114 (2018) Editor’s pick arXiv
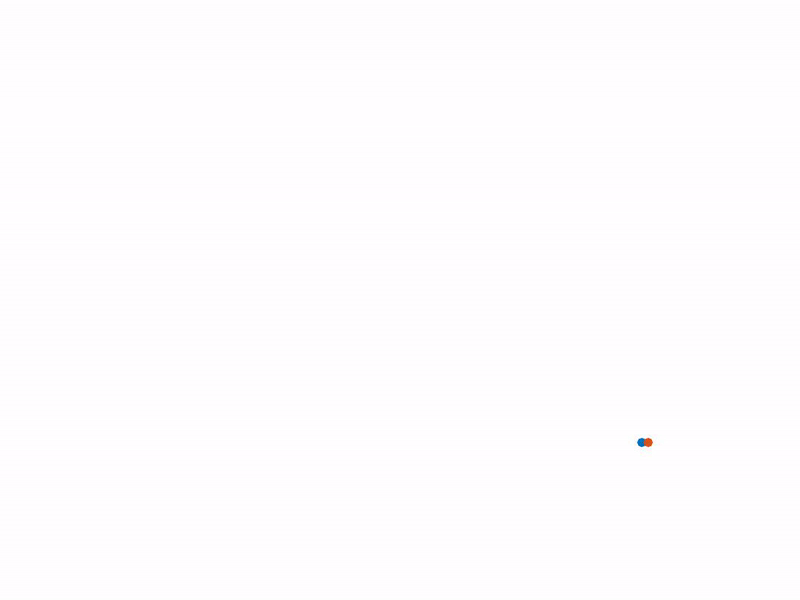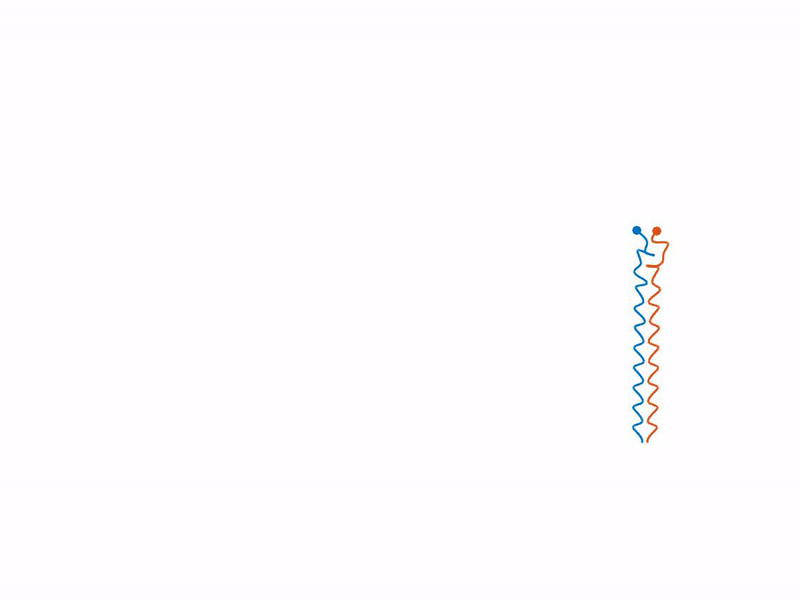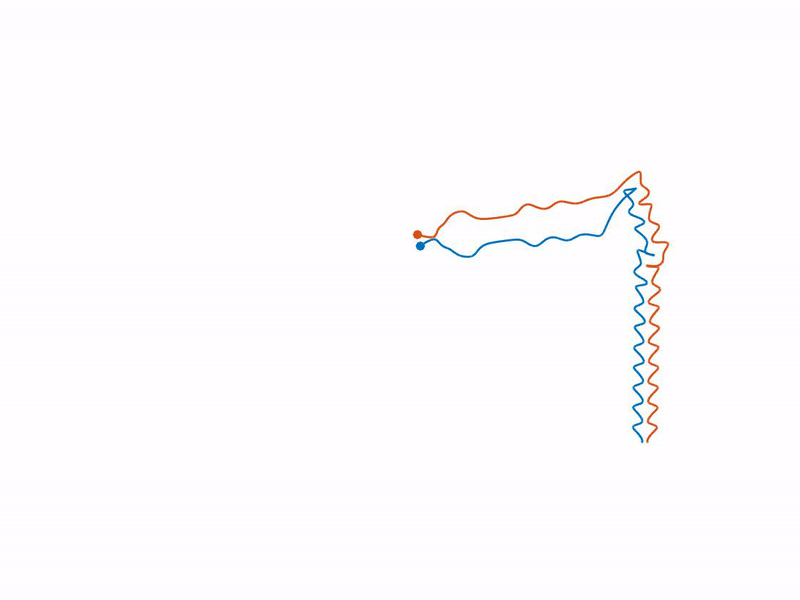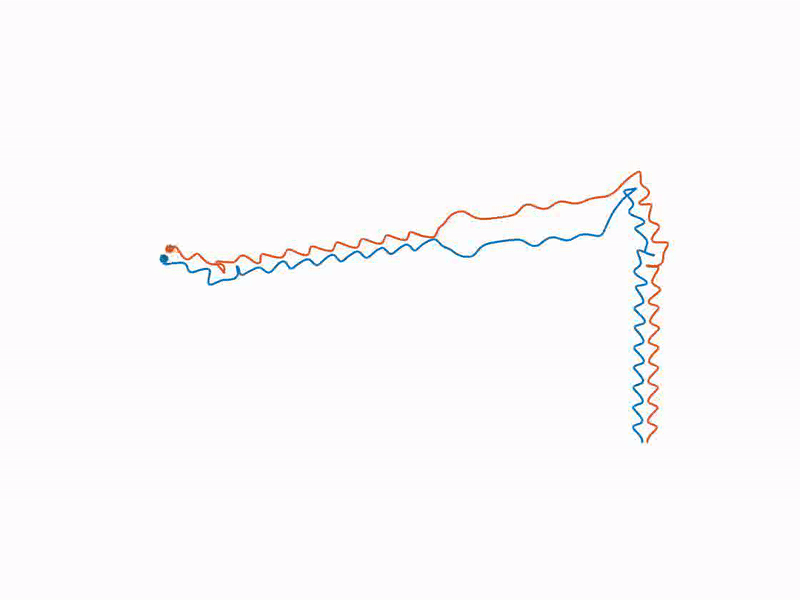
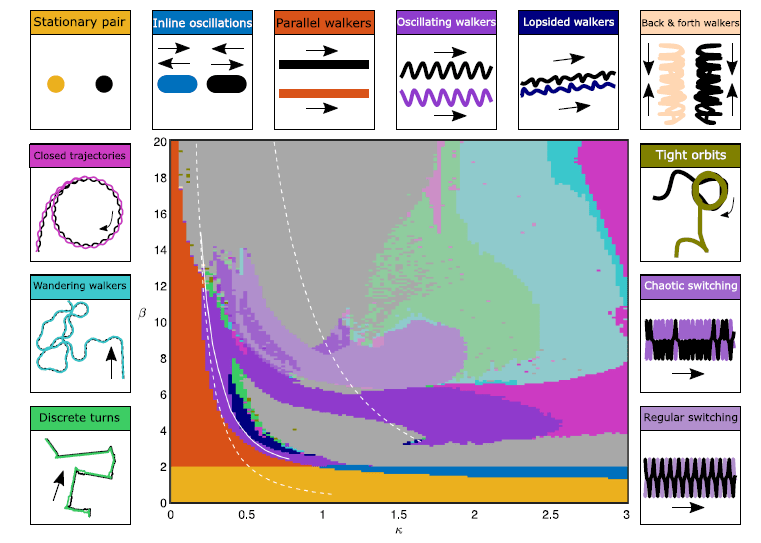
A droplet bouncing on the surface of a vibrating liquid bath can move horizontally guided by the wave it produces on impacting the bath. The wave itself is modified by the environment, and thus, the interactions of the moving droplet with the surroundings are mediated through the wave. Using a description for walking droplets as a theoretical pilot-wave model, we investigate the dynamics of two interacting identical, in-phase bouncing droplets theoretically and numerically. A remarkably rich range of behaviors is encountered as a function of the two system parameters. We explore these regimes and others and the bifurcations between them through analytic and numerical linear stability analyses and through fully nonlinear numerical simulation.
- R. N. Valani, A.C. Slim and T. Simula, Hong-Ou-Mandel-like two-droplet correlations, Chaos, 28 (9), 096104 (2018) arXiv


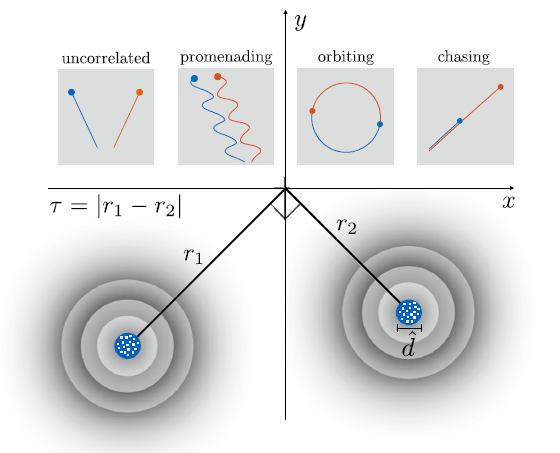
We present a numerical study of two-droplet pair correlations for in-phase droplets walking on a vibrating bath. Two such walkers are launched toward a common point of intersection. As they approach, their carrier waves may overlap and the droplets have a non-zero probability of forming a two-droplet bound state. Three generic types of two-droplet correlations are observed: promenading, orbiting, and chasing pair of walkers. For certain parameters, the droplets may become correlated for certain initial path differences and remain uncorrelated for others, while in other cases, the droplets may never produce droplet pairs. These observations pave the way for further studies of strongly correlated many-droplet behaviors in the hydrodynamical quantum analogs of bouncing and walking droplets.
- R. N. Valani, A. J. Groszek and T. Simula, Einstein–Bose condensation of Onsager vortices, New Journal of Physics, 20, 053038 (2018)
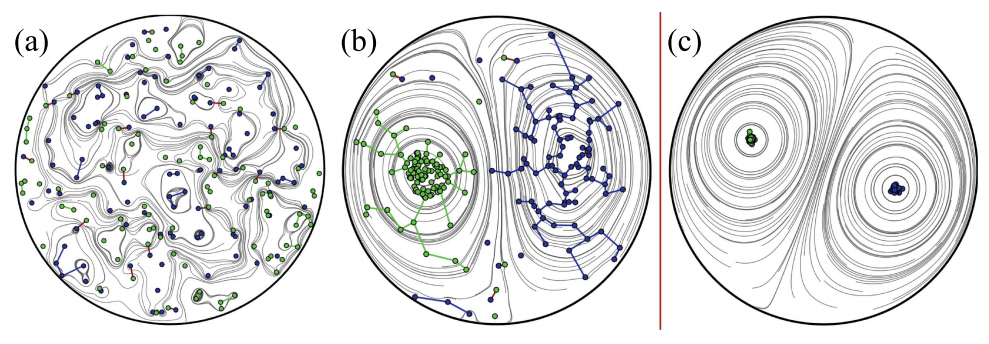
We have studied statistical mechanics of a gas of vortices in two dimensions. We introduce a new observable—a condensate fraction of Onsager vortices—to quantify the emergence of the vortex condensate. The condensation of Onsager vortices is most transparently observed in a single vortex species system and occurs due to a competition between solid body rotation (see vortex lattice) and potential flow (see multiple quantum vortex state). We propose an experiment to observe the condensation transition of the vortices in such a single vortex species system.
2016
- R. N. Valani and Kerry Hourigan, A numerical study of flow past a forced oscillating cylinder, AIAA student conference (2016)
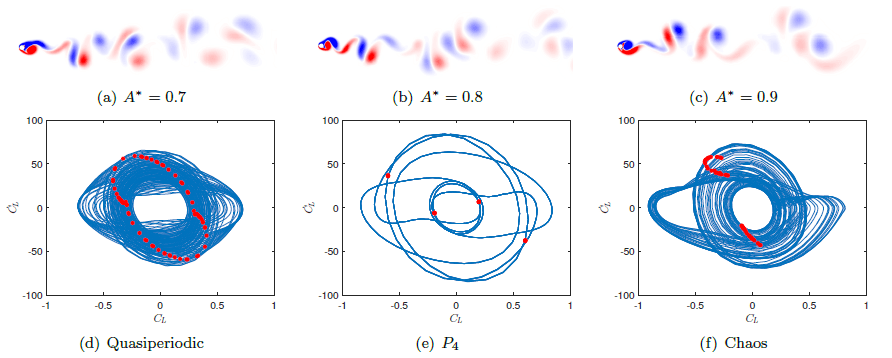
- R. N. Valani, A numerical study of flow past a forced oscillating circular cylinder at low Reynolds number, Final Year Project Thesis, Monash University (2016)

A numerical study of flow past a cylinder oscillating transverse, inline and at an angle to the incoming flow was performed at low Reynolds number. The forcing frequency and the forcing amplitude ratio were varied independently and rich dynamical responses including periodic, quasiperiodic and chaotic responses were recorded and compared to the wake topology.
.
2015
- R. Valani, A. Slim and J. Miller, Wave particle duality in multiple bouncing fluid droplets, AMSI research report (2015)
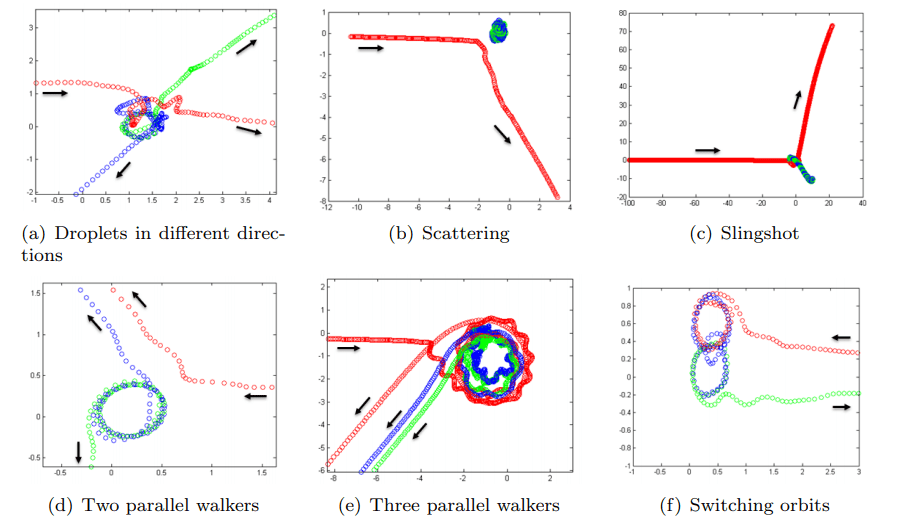
Using a simple theoretical model of a self-propelled wave-particle duality inspired from walking droplets, we theoretically and numerically explore the dynamics of two and three droplets. Using our analysis we were able to find stationary states, parallel walking states and orbiting states for two droplets as well as stationary states for three droplets which were confirmed numerically and also found experimentally. By investigating the dynamics of three droplets, various trajectories and exotic orbits were identified.
